This question is from chapter 2 polynomials class 9 maths this is the simplest question from the chapter it is a direct formula question you simply have to put the identity ( xy)^3= x^3y^33xy(xy) it is the expansion for the identity note if in place of ( xy)^3 even if ( ab)^3 is given it is the same thingNCERT Solutions Class 9 Maths Chapter 1 Number Systems Exercise 13 are provided here which are prepared by our subject experts which makes it easy for students to learn The students use it for reference while solving the exercise problems The third exercise in Number Systems Exercise 13 discusses real numbers and their decimal ExpansionExpand (1 X) 3 2marks 8 If x y z = 0 then write the value of x x y 3 z3 – 3xyz 2marks 9 Write the factors of 12 ky 2 2marks Section C 10 Represent on the number line 3marks 11 Show that can be expressed in the form 3marks 12 Visualize on the number line upto 4 decimal places 3marks 13

Expand And Simplify Binomial Squares 2x 3y 2 Youtube
Expand (1/x+y/3)^3 class 9
Expand (1/x+y/3)^3 class 9-If X 1/X = 3, then find X31/X3 Expansion Class 9 ICSE Board Learn with DebadritaHi everyoneWelcome to my channel 🙏In this Channel, I post various mat(a 3 3a 2 b 3ab 2 b 3)(ab) = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4 The calculations get longer and longer as we go, but there is some kind of pattern developing That pattern is summed up by the Binomial Theorem
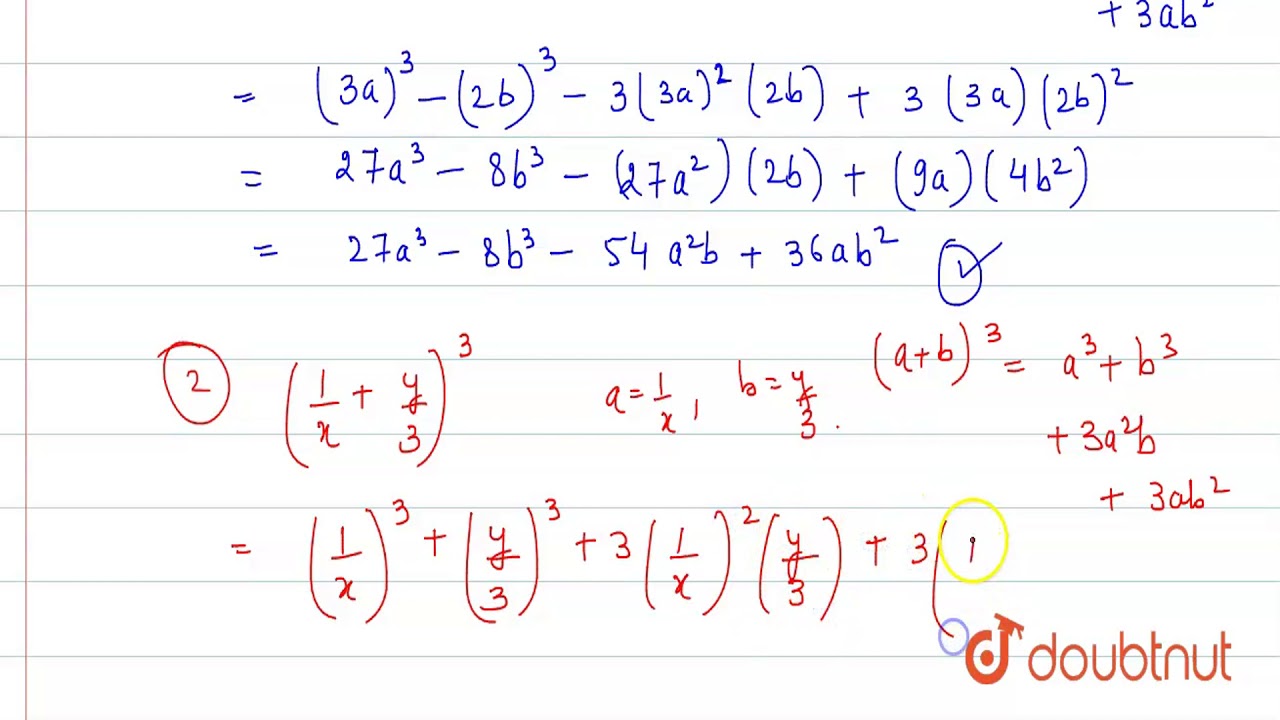



Expand The Following I 3a 2b 3 Ii 1 X Y 3 3 Iii 4 1 3x 2 Youtube
Expand Evaluate Fractions Linear Equations Quadratic Equations Inequalities Systems of Equations Matrices x 2 1 1 x 2 4 3(x3)(4x4) 3 (x − 3) (4 x − 4) x^26x160 x 2 − 6 x − 1 6 0 2x{(x6)}^{2} 2 x (x − 6) 2 3x^210x8 3 x 2The Binomial theorem tells us how to expand expressions of the form (ab)ⁿ, for example, (xy)⁷ The larger the power is, the harder it is to expand expressions like this directly But with the Binomial theorem, the process is relatively fast! কোঅফ্পিনেশন খুঁজুন `x^6y^3` সম্প্রসারণে `(x2y)^9dot` Step by step solution by experts to help you in doubt
(c) x 3 y 3 (d) x 2 y 2 Solution (b) Since, HCF is the product of the smallest power of each common prime factor involved in the numbers Question 31 The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is (a) 10 (b) 100 (c) 504 (d) 25 Solution (d) Factors of 1 to 10 numbers 1 = 1 2 = 1 x 2 3 = 1 x 3 4 = 1 xX 3 y 3 z 3 − 3 (− 1) = 1 (x 2 y 2 z 2) Expand (a b c) 3 View solution Given that, e 2 y 2 b x e y b 2 = 0 class 9 Circles Coordinate Geometry What is Democracy?Eg, since 1000 = 10 × 10 × 10 = 10 3, the "logarithm base
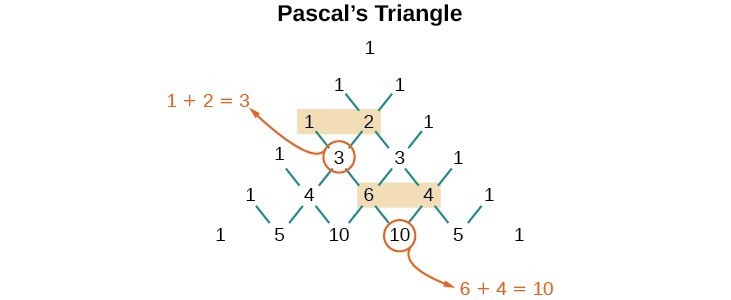
Phone support is available MondayFriday, 900AM1000PM ET You may speak with a member of our customer support team by calling End of Conversation Have a great day!To generate Pascal's Triangle, we start by writing a 1 In the row below, row 2, we write two 1's In the 3 rd row, flank the ends of the rows with 1's, and add latex11/latex to find the middle number, 2 In the latexn\text{th}/latex row, flank the ends of the row with 1'sIn mathematics, the logarithm is the inverse function to exponentiationThat means the logarithm of a given number x is the exponent to which another fixed number, the base b, must be raised, to produce that number xIn the simplest case, the logarithm counts the number of occurrences of the same factor in repeated multiplication;



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9
We can skip n=0 and 1, so next is the third row of pascal's triangle 1 2 1 for n = 2 the x^2 term is the rightmost one here so we'll get 1 times the first term to the 0 power times the second term squared or 1*1^0* (x/5)^2 = x^2/25 so not here 1 3 3 1 for n = 3 Squared term is second from the right, so we get 3*1^1* (x/5)^2 = 3x^2/25 so notThis calculator can be used to expand and simplify any polynomial expressionIn elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive




Find The Coefficient Of X 6y 3in The Expansion Of X 2y 9




Rbse Solutions For Class 9 Maths Chapter 3 Polynomial Ex 3 5
CBSE Previous Year Papers;ML Aggarwal Solutions for Class 9 Maths Chapter 3 – Expansions are provided here to help students prepare and excel in their exams This chapter mainly deals with problems based on expansions Experts tutors have formulated the solutions in a step by step manner for students to grasp the concepts easily From the exam point of view, solving the problems on a regular basis, MCQ Questions for Class 10 Maths with Answers Chapter 3 Pair of Linear Equations in Two Variables with Answers These MCQ Questions for Class 10 Maths Chapter 3 Pair of Linear Equation in Two Variables are prepared according to the latest pattern It is very helpful for students who wants to do quick revision of all the concepts related to linear equations
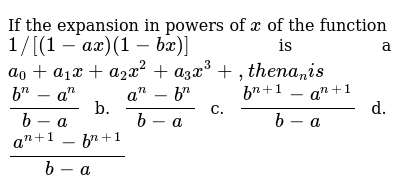



If The Expansion In Powers Of X Of The Function 1 1 A X 1 B




Using Suitable Identities Expand The Following I X5 3y 2 Ii 11x 0 2y 2 Iii 4a 5b 2 Iv Y 25x 3 V 3a 5b 4c 2 Vi 12a B 13c 2
NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations In Two Variables Exercise 43 1 Draw the graph of each of the following linear equations in two variables (i) xy = 4 Solution To draw a graph of linear equations in two variables, let us find out the points to plotSolution (i) The example of monomial of degree 1 is 5y or 10x (ii) The example of binomial of degree is 6x x 11 or x 1 (iii) The example of trinomial of degree 2 is x 2 – 5x 4 or 2x 2 x1 Question 7 Find the value of the polynomial 3x 3 – 4x 2 7x – 5, when x = 3 and also when x = 3Problems on Binomial Theorem Question 1 If the third term in the binomial expansion of equals 2560, find x Solution ⇒ (log 2x) 2 = 4 ⇒ log 2x = 2 or 2 ⇒ x = 4 or 1/4 Question 2 Find the positive value of λ for which the coefficient of x2 in the expression x2√ x



How Do You Find The Coefficient Of X 6 In The Expansion Of 2x 3 10 Socratic




Example 10 Find Term Independent Of X In 3 2 X 2 1 3x 6
Nazism and the Rise of Hitler Socialism in Europe and the Russian Revolution class 10Mathematics_ _solutions Solutions for Class 8 Math Chapter 5 Expansion Formulae are provided here with simple stepbystep explanations These solutions for Expansion Formulae are extremely popular among Class 8 students for Math Expansion Formulae Solutions come handy for quickly completing your homework and preparing for examsSample Papers Class 10 Solution;



Expand 1 X Y 3 Whole Cube Studyrankersonline




Expand 1 X Y 3 3 Solve It Fastly Brainly In
Class 10 Maths Basic vs Standard;5 Classify the following as linear, quadratic and cubic polynomials ∵ The degree of x 2 x is 2 ∴ It is a quadratic polynomial ∵ The degree of x – x 3 is 3 ∴ It is a cubic polynomial ∵ The degree of y y 2 4 is 2 ∴ It is a quadratic polynomial ∵ The degree of 1 x is 1Steps for Solving Linear Equation 3x4y=3 3 x − 4 y = 3 Add 4y to both sides Add 4 y to both sides 3x=34y 3 x = 3 4 y The equation is in standard form The equation is in standard form




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf




Expand And Simplify Binomial Squares 2x 3y 2 Youtube
NCERT Solutions for Class 9 Maths Chapter 2 has 5 exercises The topics discussed in these exercises are polynomials in one Variable, zeros of a polynomial, real numbers and their decimal expansions, representing real numbers on the number line and operations on real numbers laws of exponents for real numbersFind the zeros of the polynomial p (x) = 4 x 2 – 25 If abc = 0, thenML Aggarwal Solutions for Class 9 Maths Chapter 3 – Expansions Exercise 31 By using standard formulae, expand the following (1 to 9) 1 (i) (2x 7y)2 (ii) (1/2 x 2/3 y)2 Solution




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf
Rs_aggarwal_18 Solutions for Class 9 Math Chapter 3 Factorisation Of Polynomials are provided here with simple stepbystep explanations These solutions for Factorisation Of Polynomials are extremely popular among Class 9 students for Math Factorisation Of Polynomials Solutions come handy for quickly completing your homework and preparing for examsNCERT Solutions for Class 9 Maths Chapter 5 Factorization Of Algebraic Expressions are provided here with simple stepbystep explanations These solutions for Factorization Of Algebraic Expressions are extremely popular among Class 9 students for Maths Factorization Of Algebraic Expressions Solutions come handy for quickly completing your homework and preparing for examsFind the coefficient of a 3 in the expansion of (2 a – 5) 3 Find the value of polynomial 4x 2 – 5x 9, when x = 1 2;




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5
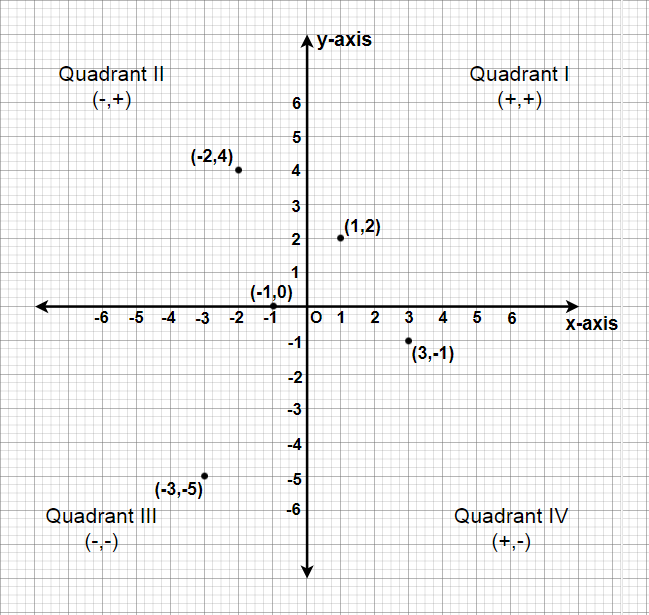



Class 9 Ncert Solutions Chapter 3 Coordinate Geometry Exercise 3 3 Geeksforgeeks
The coefficient of x3y4z in the expansion of (1 x y −z)9 is The coefficient of x 3 y 4 z in the expansion ofFind the coefficient of y in the expansion of (2y – 3) 3 Find the value of 1015 2 – 1014 2 Find the zero of the polynomial p(x) = 4 – 5x;R S Aggarwal and V Aggarwal Solutions for Class 9 Mathematics CBSE, 3 Factorisation of Polynomials All the solutions of Factorisation of Polynomials Mathematics explained in detail by experts to help students prepare for their CBSE exams



Mrurbanc Weebly Com Uploads 4 4 2 6 Pages From Hl Exam Review Assignment Answers Part 1 Pages 01 Pdf




Expand X 1 Y 11 Y 0
ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 3 Expansions Chapter Test Question 1 Find the expansions of the following (i) (2x 3y 5) (2x 3y – 5) Question 5 Find the remainder when x 3 x 2 x 1 is divided by x – using remainder theorem Solution Let p (x) = x 3 x 2 x 1 and q (x) = x – Here, p (x) is divided by q (x) ∴ By using remainder theorem, we have Question 6 Find the common factor in the quadratic polynomials x 2 8x 15 and x 2 3x – 10 Question 5 Find the remainder when x 3 x 2 x 1 is divided by x – using remainder theorem Solution Let p (x) = x 3 x 2 x 1 and q (x) = x – Here, p (x) is divided by q (x) ∴ By using remainder theorem, we have Question 6 Find the common factor in the quadratic polynomials x 2 8x 15 and x 2 3x – 10




1 Expand Y 3 X 2 Brainly In




Example 10 Find Term Independent Of X In 3 2 X 2 1 3x 6
Steps for Solving Linear Equation x2y = 10 x 2 y = 1 0 Subtract x from both sides Subtract x from both sides 2y=10x 2 y = 1 0 − x Divide both sides by 2 Divide both sides by 2Expand each of the following, using suitable identities (i) (x 2 y 4 z) 2 (ii) (2 x − y z) 2 (iii) (− 2 x 3 y 2 z) 2 (iv) (3 a − 7 b − c) 2 (v) (− 2 x 5 y − 3 z) 2 (vi) 4 1 a − 2 1 b 1 2QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by highschool and college students The algebra section allows you to expand, factor or simplify virtually any expression you choose It also has commands for splitting fractions into partial fractions, combining several fractions into one and



1




Taylor Series Wikipedia
Sample Papers Class 12 Solution;Y = 3 x 4 Arithmetic 699 * 533 6 9 9 { 1 } x e ^ { x ^ { 2 } } d x Algebra Combine Like Terms Solve for a Variable Factor Expand Evaluate Fractions Linear Equations Quadratic Equations Inequalities Systems of Equations Matrices Trigonometry Simplify Evaluate Graphs Solve Equations Calculus Sample paper for class 9 maths periodic test 1 116 Class 9 Sample Paper Math Know about the important concepts to be prepared for CBSE Class 9 Maths board exam and Score More marks Write the degree of polynomial 2 y 2 y 3 2y 8 Click to access mathsclassxperiodictestiiisamplepaper02pdf 125 on the number line



Who Can Solve This X Y 15 And X Y 3 Find X And Y Quora




Expand 1 X Y 3 3 Novocom Top
Algebraic Identities For Class 9 With Examples Now that we have provided all the formulas of Algebra Class 9, let's see some examples on the same Question 3 If m 1/m = 11, find the value of m2 1/m2 Answer Using identity (x y z) 2 = x 2 y 2 z 2 2xy 2yz 2xz, we can expand the algebraic expressions1 x 2 = (3 2i) x 1 x 2 )2ix 2 = x 1 For x 2 = 1 we obtain x(1) = (2i 1 Finally for the second eigenvalue 2, the eigenvector is x(2) = 2i i Math 331 Homework Assignment Chapter 7 Page 4 of 9 4 For the system of di erential equations x0= Ax A = 2 5 1 2 and the two vectorvalued functions x 1(t) = 5cost 2cost sint ; Example 22 Write the following cubes in the expanded form (3a 4b)3 (3a 4b)3 Using (x y)3 = x3 y3 3xy(x y) Where x = 3a & y = 4b = (3a)3 (4b)3 3(3a)(4b)(3a 4b) = 27a3 64b3 3(3a)(4b)(3a) 3(3a)(4b) (4b) = 27a3 64b3 108a2b 144ab2 Example 22 Write the Chapter 2 Class 9 Polynomials Last updated at by




Expand 1 3x 2 5y Brainly In



Who Can Solve This X Y 15 And X Y 3 Find X And Y Quora
এর সহগ `x^2y^3` সম্প্রসারণে `(1xy)^()` হয় `( !)/(213 !)` খ। `( !)/(213 !)` গ। `( !)/(5!2!3!)` ঘCBSE Datesheet Boards; Transcript Ex 25, 6 Write the following cubes in expanded form (i) (2x 1)3 (2x 1)3 Using (a b)3 = a3 b3 3ab(a b) Where a = 2x & b =1 = (2x)3 (1)3 3(2x)(1) (2x 1) = 8x3 1 6x(2x 1) = 8x3 1 12x2 6x = 8x3 12x2 6x 1 Ex 25, 6 Write the following cubes in expanded form (ii) (2a 3b)3 (2a 3b)3 Using (x y)3 = x3 y3 3xy(x y) Where x = 2a & y = 3b = (2a)3




Please Expand 1 X Y 3 Whole Cube Brainly In




Binomial Theorem Wikipedia
MCQ Questions for Class 9 Maths Chapter 2 Polynomials with answers 1 Factorise 8a 3 b 3 12a2b 6ab 2 2 The value of k for which x 1 is a factor of the polynomial x3 x2 x k is 3 Using Remainder Theorem find the remainder when x3 x2 x 1 is divided by x Find the coefficent of`x^(6)y^(3)` in the expansion of `(x2y)^(9)` Step by step solution by experts to help you in doubt clearance & scoring excellent marks in exams* Numerically greatest term in the expansion of (1 x) n i) If ( 1) 1 n x x = p, a integer then p th and (p 1) th terms are the numerically greatest terms in the expansion of (1 x) n ii) If 9 9 4 5 6 5 5 2x 3y 2 3 T C C x y 3 2 3 x




Taylor Series Wikipedia




Expanding Binomials Video Polynomials Khan Academy
After having gone through the stuff given above, we hope that the students would have understood "How to Find Coefficient of x in Binomial Expansion"Apart from the stuff given above, if you want to know more about "How to Find Coefficient of x in Binomial Expansion" Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search hereCBSE Sample Papers 21;




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf
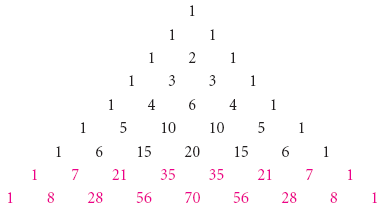



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets




The Greatest Binomial Coefficient In The Expansion Of X 3 2 Y



What Is The Binomial Expansion Of Math 1 X 2 Math Quora
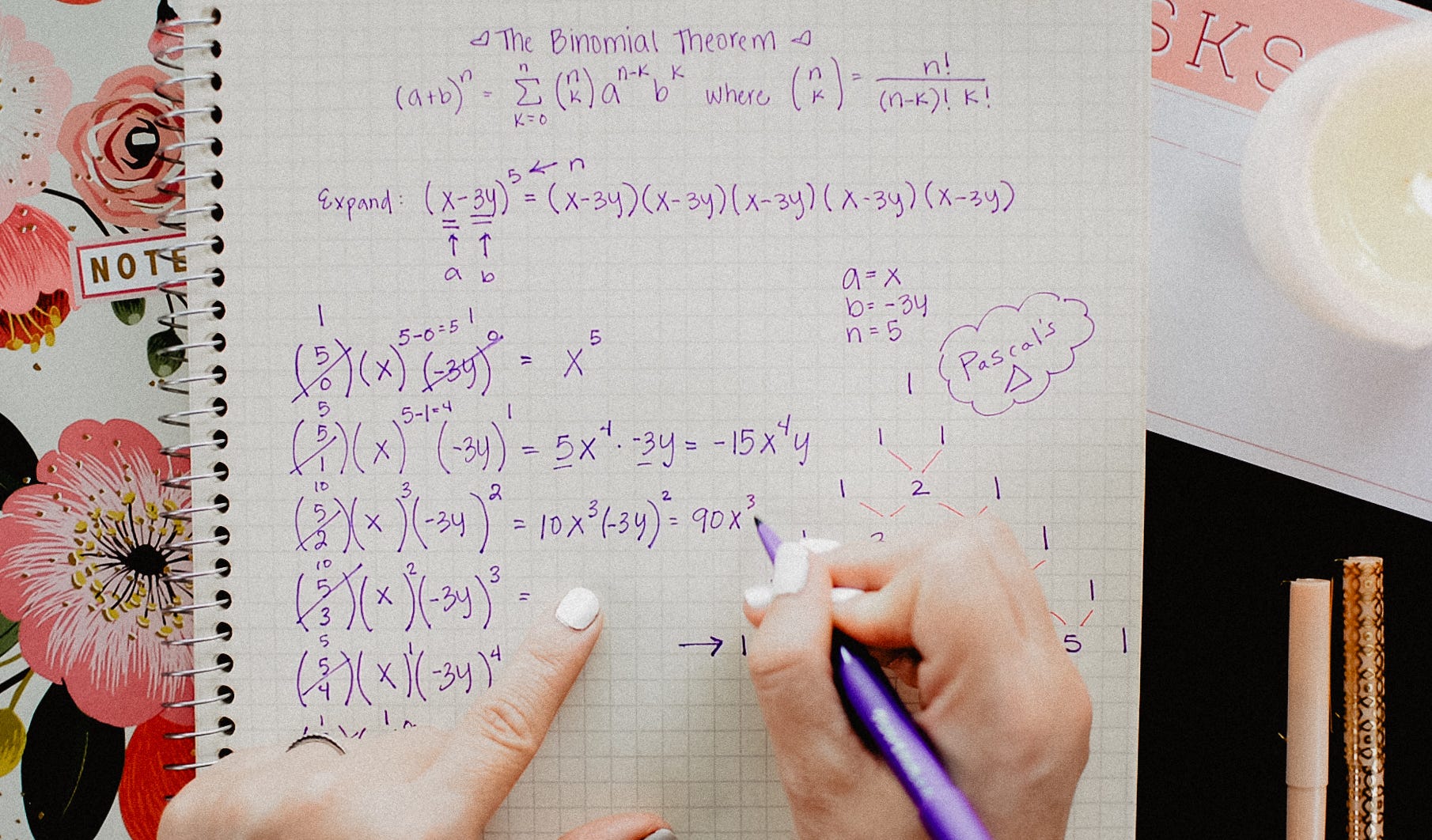



The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium




The Binomial Coefficient Of The Third Term Of The End In The Expansion Of Y 2 3 X 5 4 N Is 91 Find The Ninth Term Of The Expansion




Binomial Theorem For Any Index




Find The Constant Term In The Binomial Expansion Of 2x 7 X 2 21 Youtube




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com
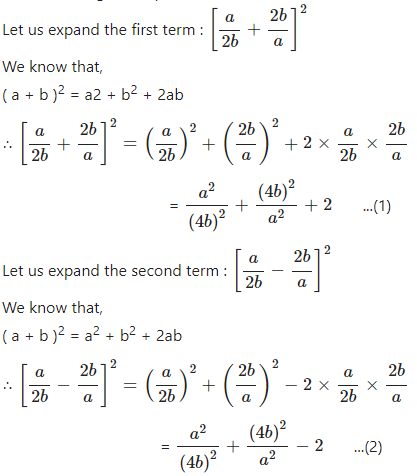



Expansions Icse Class 9th Concise Selina Mathematics Icsehelp




1 X Y 3 3 Expand Brainly In




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube
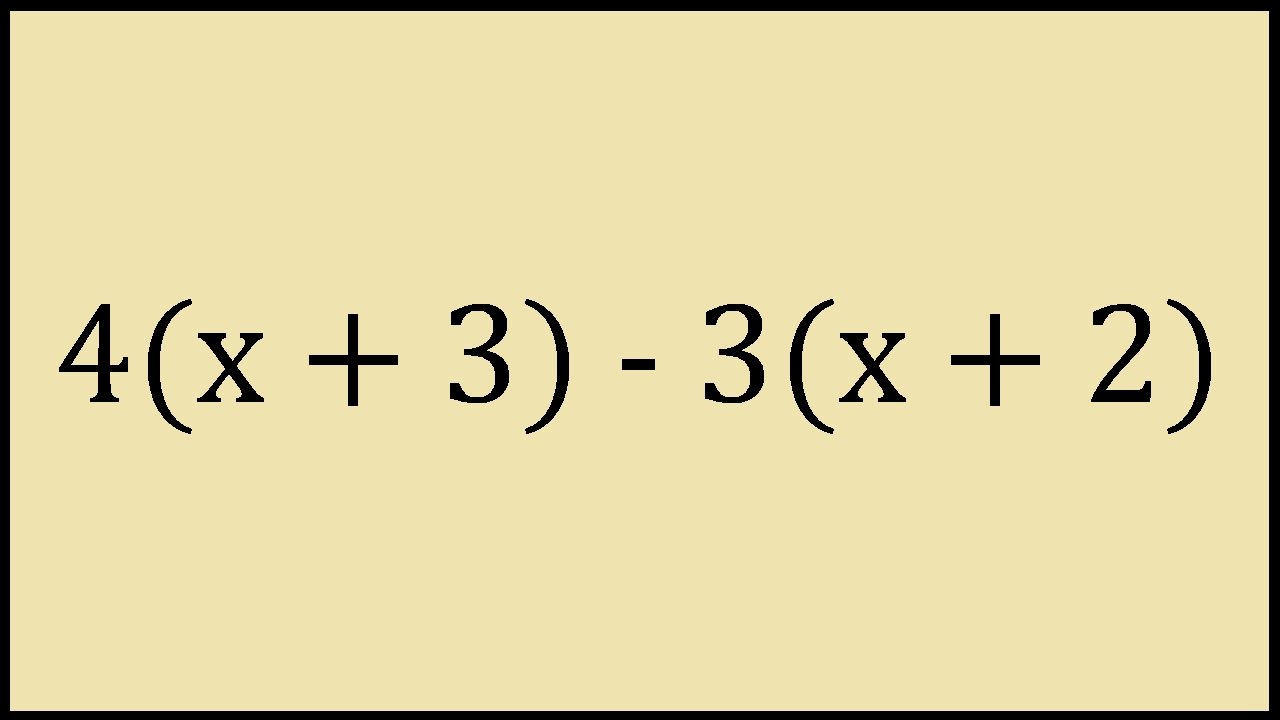



4 X 3 3 X 2 Expand And Simplify Youtube




Algebraic Identities Of Polynomials A Plus Topper




Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths



Q Tbn And9gcqw3ytr8shmxjcu2 37v8gqgdbytzhzbbgxwcuepfumanvsy3e4 Usqp Cau




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5
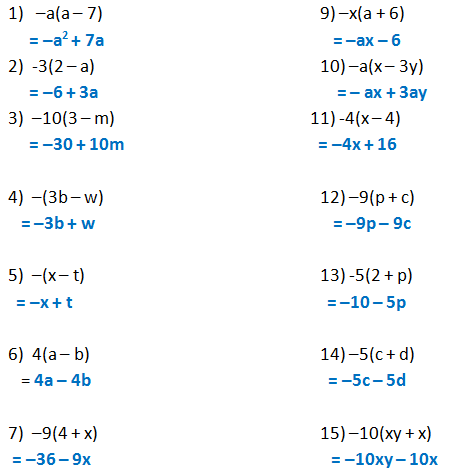



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths




The Binomial Theorem Fractional Powers Expanding 1 2x 1 3 Youtube




Algebraic Identities Of Polynomials A Plus Topper
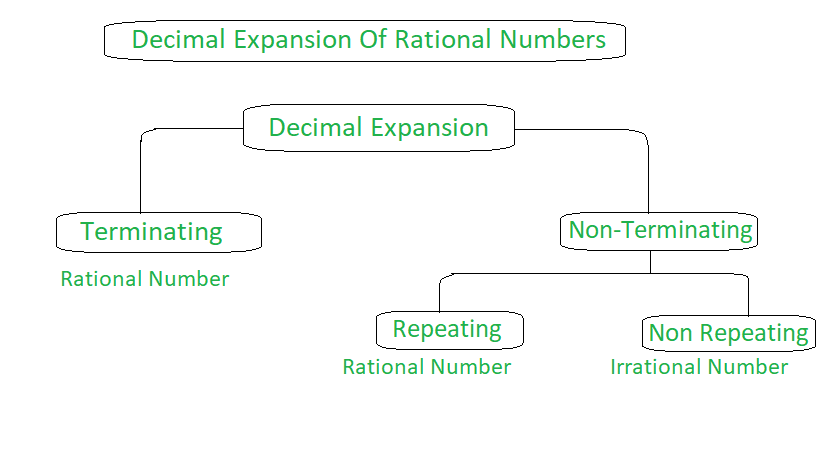



Decimal Expansion Of Real Numbers Geeksforgeeks




Expand 1 3 X 2 3 Y Whole Cube Brainly In




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials




Example 8 The 2nd 3rd 4th Terms In Expansion X A N Are 240
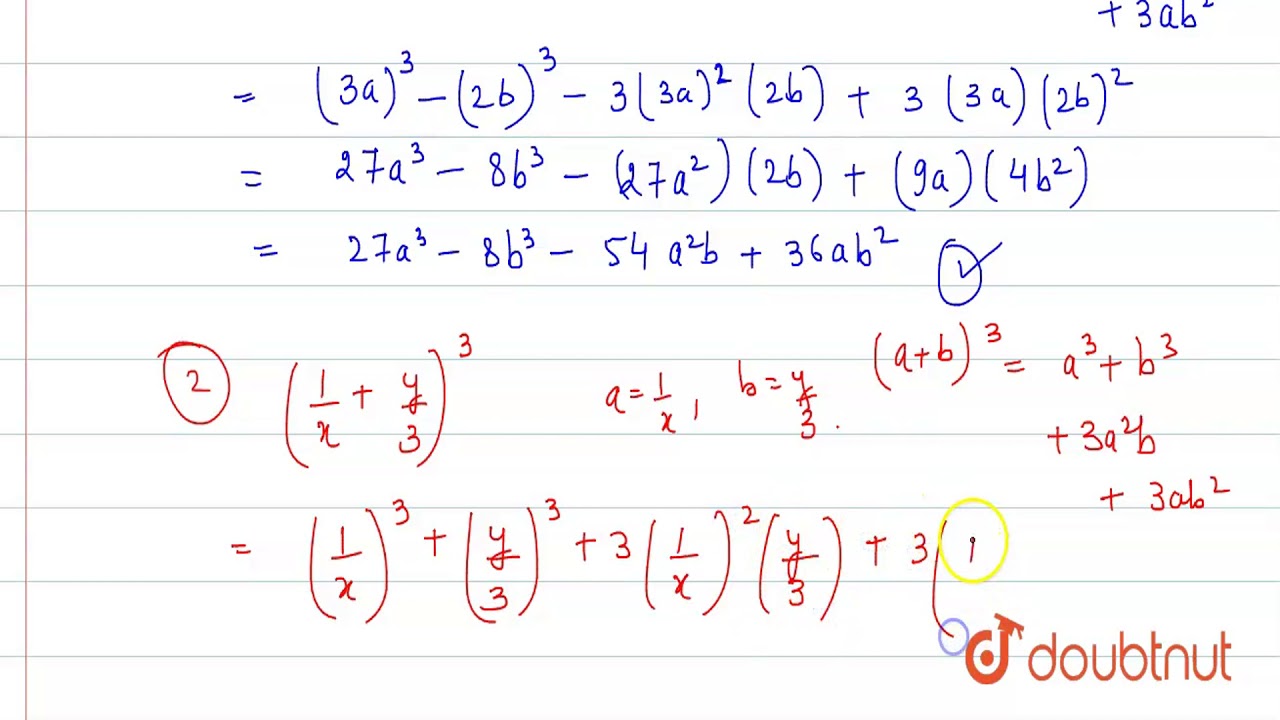



Expand The Following I 3a 2b 3 Ii 1 X Y 3 3 Iii 4 1 3x 2 Youtube



Use The Binomial Theorem College Algebra




Number Of Terms In Expansion Of Following I 2x 3y 9 Ii 2x 3y 4z N
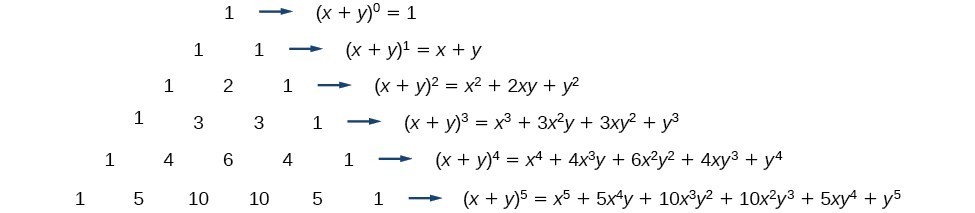



Use The Binomial Theorem College Algebra




Example 10 Find Term Independent Of X In 3 2 X 2 1 3x 6




X 2 2y 3 1 X Y 3 3 Solve The Given Equation Using Elimination And Substitution Method Youtube



Q Tbn And9gctrpod5wp0yfbr8op Svklbrvw6frcvhr0kqyrjgtgvhuqyyxiu Usqp Cau




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5
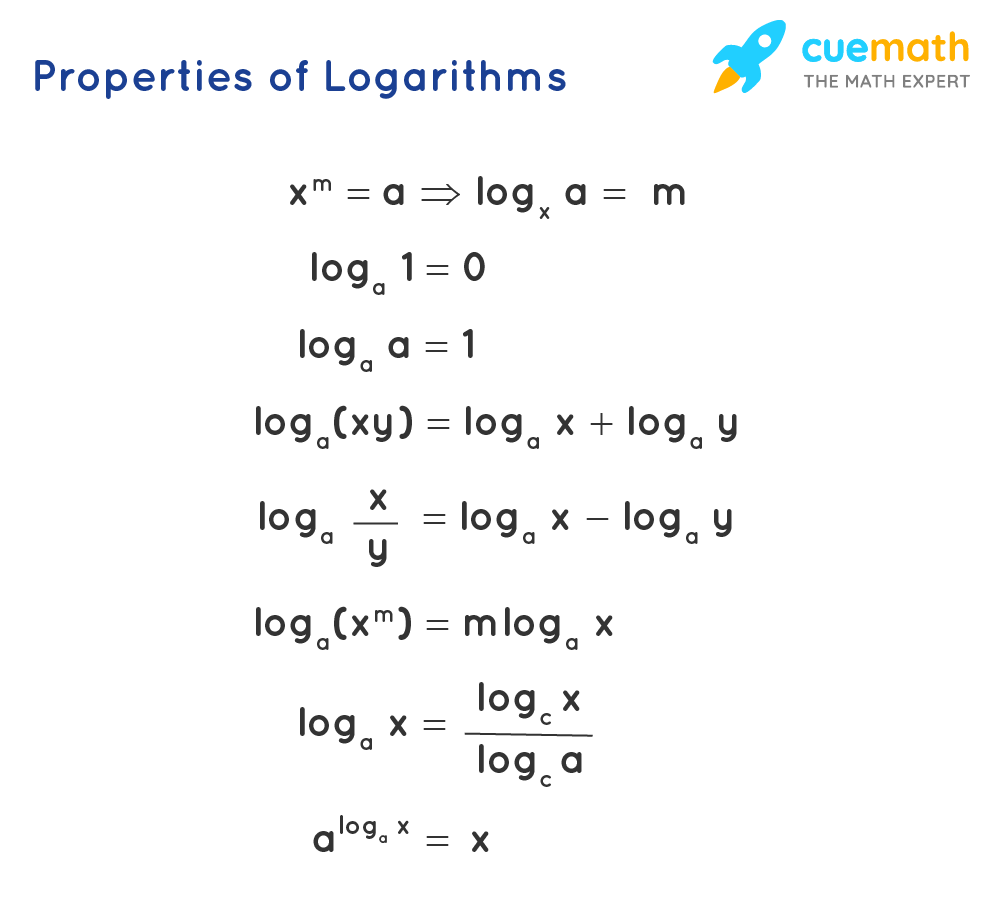



Algebra Formula Solved Examples List Of Algebraic Formulas




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com




Section 9 Binomial Expansion Questions About Homework Submit Homework Recall The Exercises We Did Last Class 04 01 19 Math 106 Section 9 1 Slideshow And Powerpoint Viewer What Is Binomi




Pc 9 5 Ppt 9 5 The Binomial Theorem Let U19s Look At The Expansion Of X Y N X Y 0 1 X Y 1 X Y X Y 2 X2 2xy Y2 X Y 3 X3 3x2y 3xy2 Y3 X Y 4 X4 Course Hero



Form 2 Unit 2 Lesson 5 Expansion Of Algebraic Expression Brilliant Maths




Taylor Series Expand X 2y 3y 2 In The Powers Of X 1 And Y 2 Up To 3 Degree Terms Youtube




Please Expand 1 X Y 3 Whole Cube Brainly In




Write The Following Cubes In The Expanded Form I 3a 4b 3




Expand 1 X Y 3 3 Novocom Top




Class 9ncert Solutionschapter 2 Polynomialsexercise 2 5 Solve All Questions And Give Me Answersplease Brainly In



4 The Binomial Theorem




Expand X Y 3 And X Y 2 Brainly In




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube




Taylor Series Wikipedia



Www Shorelineschools Org Cms Lib Wa Centricity Domain 18 Math 5 11 copy Pagenumber Pdf




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf




Expand X X Y 3 3xy X Y




The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets




9 Binomial Theorem Example 4 Expanding 3 Terms In A Binomial Question Youtube



What Is The Answer Of X Y Quora
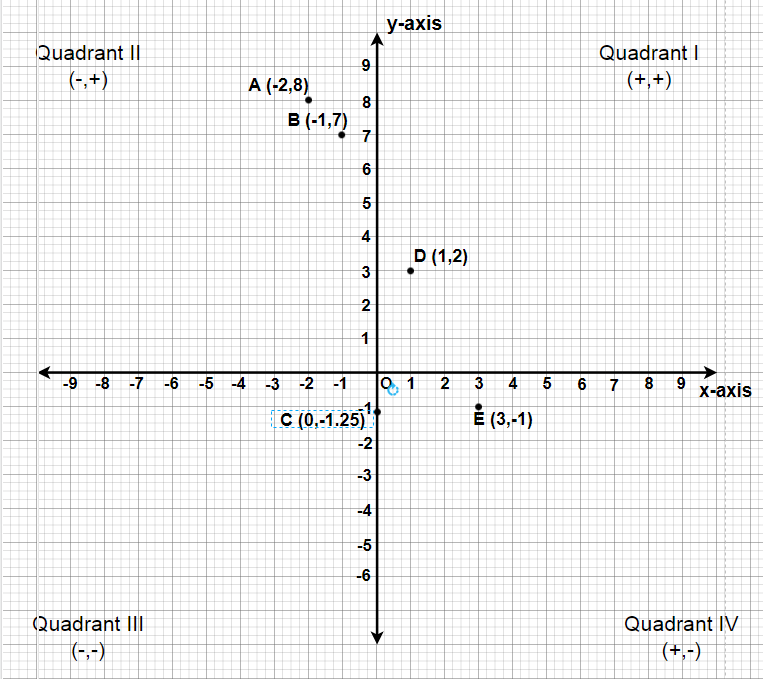



Class 9 Ncert Solutions Chapter 3 Coordinate Geometry Exercise 3 3 Geeksforgeeks




Example 5 Solution Simplify 2x 3y 4z 4x2 9y2 1622 1622 We Know That A B C A 62 C2 Ab




Selina Solutions Class 9 Concise Maths Chapter 5 Factorisation Download Free Pdf




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5




Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities




Expand Using Identity 2x 3y 3




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf




Algebraic Identities Of Polynomials A Plus Topper




Class 9ncert Solutionschapter 2 Polynomialsexercise 2 5 Solve All Questions And Give Me Answersplease Brainly In




Pearson Maths Class 9 Solution Fraction Mathematics Abstract Algebra




Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf




Find The Coefficient Of X 2 Y 3 Z 4 In The Expansion Of Ax By



If Math X Y 3 Math And Math X 2 Y 2 3 Math Then What Is The Value Of Math X 2 Y 2 Math Quora




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf




Binomial Theorem Wikipedia




Use The Binomial Theorem College Algebra




Expand 1x Y3 3 Maths Questions




How To Use The Binomial Theorem In 1 X 1 2 Quora



No comments:
Post a Comment