Solution for X^36x^211x6= equation Simplifying X 3 6x 2 11x 6 = 0 Reorder the terms 6 X 3 11x 6x 2 = 0 Solving 6 X 3 11x 6x 2 = 0 Solving for variable 'X' Move all terms containing X to the left, all other terms to the rightIf there is more than one answer, give all of the xvalues separated by commas, eg if f (x) has a tangent line of slope −3 at x=3 and x=5 enter 3,5 Use fractions if necessary, do not enter decimal valuesThis video shows an example of graphing a polynomial function with a highest degree that is odd
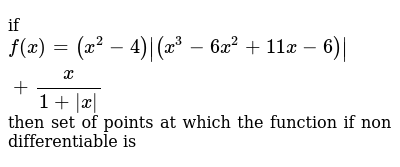
If F X X 2 4 X 3 6x 2 11x 6 X 1 X Then Set Of Points At Which The Function If Non Differentiable Is
F(x)=x^3-6x^2 11x-6 g(x)=x-3
F(x)=x^3-6x^2 11x-6 g(x)=x-3- 10 POINTS BRAINLIEST ANSWER!!By inspection, x = 1 is a zero so (x1) is a factor By synthetic division x^3 6x^2 11x 6 = 0 → (x 1)(x^2 5x 6) = 0 For the quadratic factor 6 = 2*3 → 23 = 5 The quadratic factors nicely
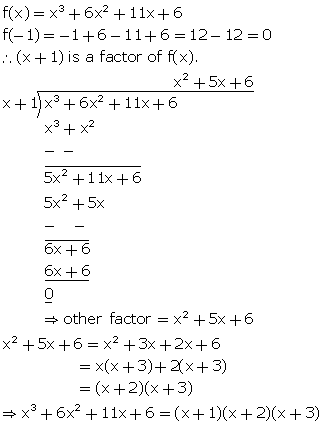



Factorize X3 6x2 11x 6 Mathematics Topperlearning Com Iv3dg99oo
A h(x) = 12 11x 2 B h(x) = x2 – 11x2 C h(x) = x2 x – 4 D h(x) = 3r2 x – 4 E h(x) = x2 x2 Categories Mathematics Leave a Reply Cancel reply Your email address will not be published Required fields are marked * CommentSOLUTION Given f(x)=x^36x^211x6 Show that f(2)=0 and find the three factors of f(x)X 3 6x 2 11x = x • (x 2 6x 11) Trying to factor by splitting the middle term 42 Factoring x 2 6x 11 The first term is, x 2 its coefficient is 1 The middle term is, 6x its coefficient is 6 The last term, "the constant", is 11 Step1 Multiply the coefficient of the first term by the constant 1
Find an answer to your question f(x)=x^36x^211x6,g(x)=x2 See answers priyankakri9058 priyankakri9058 priyankakri9058 Explanation Rolle's theorem states that if a function f (x) is continuous on the interval a,b and differentiable on the interval (a,b) and if f (a) = f (b) then there exists c ∈ (a,b) such that f '(c) = 0 Here, f (x) = x3 − 6x2 11x −6 The interval is I = (1,3) f (1) = 13 − 6 × 12 11 × 1 −6 = 0 f (3) = 33 − 6 × 32 11 × 3 −6 = 0 F(x)=x^36x^211x6,g(x)=x^2x1 Get the answers you need, now!
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreAnswer Let f (x) = x3 −6x2 11x−6 and p(x) = x−2 Dividing f (x) by p(x) we get Quotient q(x) = x2 −4x3 and Remainder r(x) = 0 p(x)q(x)= (x−2)(x2 −4x3) p(x)q(x)= x3 −4x2 3x−2x2 8x−6 p(x)q(x)= x3 −6x2 11x−6 ⇒ p(x)q(x) = f (x) ⇒ p(x)q(x)0= f (x) ⇒ p(x)q(x)r(x) = f (x)Group 1 11x 3 6 Group 2 x 5 6x 4 Pull out from each group separately Group 1 (11x 3 6) • (1) Group 2 (x 6) • (x 4) Bad news !!




How To Factor Math X 3 6x 2 11x 6 0 Math Quora



If A Is Domain Of F X In Tan 1 X 3 6x 2 11x 6 Sarthaks Econnect Largest Online Education Community
Factoring by pulling out fails The groups have no common factor and can not be added up to form a multiplication Polynomial Roots Calculator 54 Find roots (zeroes) of F(x) = x 5 6x 4 11x 3 6 (fg) (x) =f(x) g(x) = x^32x^212x6(4x^2 6x4)= x^32x^212x64x^26x4= x^36x^218x10 msm555 msm555 Answer Solution given f(x)=x3−2x212x−6 g(x)=4x2−6x4 now (fg)(x)=f(x)f(g)=x3−2x212x−64x²6x4 =x³6x²18x10 New questions in Mathematics 16A piece of cloth costs Birr 0 If the piece was 5 m longer, and the f(x) = x 3 6x 2 11x 6 and g(x) = x 1 Clearly, degree of f(x) = 3 and degree of g(x) = 1 Therefore, the degree of quotient is q(x) = 3 1 = 2 and the degree of remainder is r(x) = 0 Let quotient q(x) = ax 2 bx c and remainder r(x) = k Using division algorithm, we have f(x) = g(x) × q(x) r(x)



Factorize X 6x 3x 10 Quora
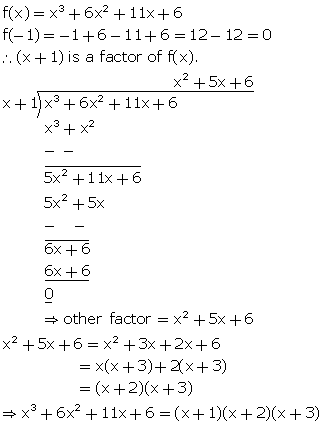



Factorize X3 6x2 11x 6 Mathematics Topperlearning Com Iv3dg99oo
Solution Steps g ( x ) = x ^ { 3 } 2 x ^ { 2 } 11 x 6 g ( x) = x 3 − 2 x 2 − 1 1 x − 6 By Rational Root Theorem, all rational roots of a polynomial are in the form \frac {p} {q}, where p divides the constant term 6 and q divides the leading coefficient 1 One such root is 2 Factor the polynomial by dividing it by x2Calculadoras gratuitas passo a passo para álgebra, trigonometria e cálculoF(x) = x^3−2x^2−11x+12 Extended Keyboard;




R D Sharma Class 10 Solutions Maths Chapter 2 Polynomials Exercise 2 3




Factorise X3 6x2 11x 6 Using Factor Theorem Brainly In
If the function f(x) = ax^3 bx^2 11x 6 satisfies the conditions of Rolle's theorem for the interval 1,3 and f'(2 1/√3) = 0, then the values of a and b are respectively23 Find roots (zeroes) of F(x) = x 36x 211x6 Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F(x)=0 Rational Roots Test is one of the above mentioned tools It would only find Rational Roots that is numbers x which can be expressed as the quotient of two integers TheGraph f(x)=x^36x^211x6 Find the point at Tap for more steps Replace the variable with in the expression Simplify the result Tap for more steps Simplify each term Tap for more steps Raising to any positive power yields Raising to any positive power yields Multiply by



2




Numerical Methods For The Root Finding Problem Pdf Free Download
Calculadoras gratuitas paso por paso para álgebra, Trigonometría y cálculoHow do you factor x^3 6x^2 11x 6 = 0 ? If x^36x^211x6 is a prime number then number of possible integral values of x is Updated On 214 To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!



Www Lcps Org Cms Lib4 Va Centricity Domain 4777 Test key unit 5 Pdf




Solved Determine The Highest Real Root Of F X X 3 6x 2 11x 6 1 1 Answer Transtutors
বহুবর্ষীয় এফ (এক্স) = x ^ 3 6x ^ 2 11x 6 এর অবিচ্ছেদ্য শিকড় খুঁজে 306kIt is given that f(x) = x 3 − 6x 2 11x − 6, and g(x) = x 2 − 3x 2 We have g(x) = x 2 − 3x 2 ` = x^2 2x x 2` ` = (x 2) (x1)` \\Rightarrow \left( x 2 \right)\ and (x − 1) are factor of g(x) by the factor theorem To prove that (x − 2) and (x − 1) are the factor of f(x)For which value (s) of x does f (x)=3x^33x^2−11x−1 have a tangent line of slope −3?




Using Factor Theorem Show That G X Is A Factor Of P X When P X 2x 4 9x 3 6x 2 11x 6 G X X 1



How Do You Use The Graph Of F X X 3 6x 2 11x 6 To Rewrite F X As A Product Of Linear Factors Socratic
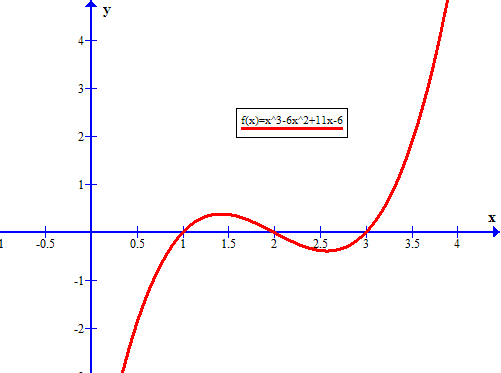
Determine the highest real root of (x) = x 3 6x 2 11x 61 (a) Graphically (b) Using the NewtonRaphson method (three iterations, x 0 = 35 (c) Using the secant method (three iterations, r 1 = 25 and x 0 = 35) (d) Using the modified secant method (three iterations, x 0 = 35, δ = 001) (e) Determine all the roots with MATLAS x^36x^211x6=color(red)((x1)(x2)(x3)) There are several ways to approach this One of the most reliable is to hope that the expression has rational roots and apply the Rational Root Theorem In this case, the Rational Root Theorem tells us that (if the expression has rational roots) those roots are integer factors of 6 (the constant term of the expression)Subtract 6 6 from 1 1 Multiply 11 11 by 1 1 Add − 5 5 and 11 11 Subtract 6 6 from 6 6 Since 1 1 is a known root, divide the polynomial by x − 1 x 1 to find the quotient polynomial This polynomial can then be used to find the remaining roots Divide x 3 − 6 x 2 11 x − 6 x 3 6 x 2 11 x 6 by x − 1 x
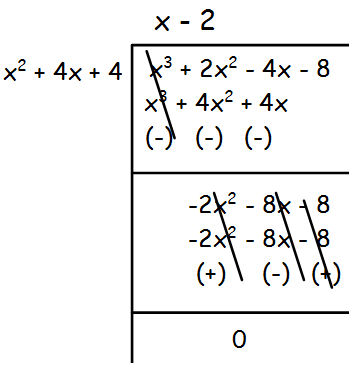



Gcd Of Polynomials Using Division Algorithm



Using Division Algorithm Find Quotient And Remainder Dividing F X By G X I F X 3x 3 X 2 2x 5 G X 1 2x X 2 Sarthaks Econnect Largest Online Education Community
611x6x^2x^3=0 2x^5x^42x1=0 116xx^2=\frac {6} {x} x^32x=0 2x^5x^42x1=0 polynomialequationcalculator 611x6x^2x^3=0 F(x) = 2×2 – 5x3 8(x) = x2 6x1 What is h(x) if h(x) = g(x)f(x)?Question 1 f(x) = x 3 – 6x 2 11x – 6;




X 3 6x 2 11x 6 क ग णनखण ड क ज ए




R D Sharma Class 10 Solutions Maths Chapter 2 Polynomials Exercise 2 3
Let f(x) = x^3 6x^2 11x 6 Try x = 1: f(1) = 1 6 11 6 = 0 So x 1 is a factot of f(x) Try x = 2: f(2) = 8 24 22 6 = 0 In each of the following, g(x) is a factor of polynomial f(x) or, not f(x) = x^3 6x^2 11x 6, g(x) = x 3 asked Apr in Polynomials by Daivi (Factorx^{3}6x^{2}11x6 he Related Symbolab blog posts Practice Makes Perfect Learning math takes practice, lots of practice Just like running, it takes practice and




Factorise X 3 6x 2 11x 6



Q Tbn And9gcsjcugx5pkoowy3 Cjavlyoito0xc2svvhtwt2b8zeniasxlz9o Usqp Cau
Factorise The given Polynomial Find what must be subtracted from 4y412y36y250y26 so that obtained polynomial is exactly divisible by y24y2 Factorise 2u33u217u30 Using factor theorem factorise the polynomial x rays to 4 x rays to 3 7x rays to 2 x 6 Find integral zeros of 2xcube 3xsquare 8x12G(x) = x – 3 Solution If g(x) is a factor of f(x), then the remainder will be zero that is g(x) = 0 g(x) = x 3 = 0 or x = 3 Remainder = f(3) Now, f(3) = (3) 3 – 6(3) 2 11 x 3 – 6 = 27 – 54 33 – 6 = 60 – 60 = 0 Therefore, g(x) is a factor of f(x) Question 2 f(x) = 3X 4 17x 3Click here👆to get an answer to your question ️ Divide x^3 6x^2 11x 6 by x^2 x 1




Problem 40 The Value S Of A For For Which X3 6x2 Math




Chapter 8 Polynomials Government Of Karnataka Solutions For Class 10 Mathematics Maharashtra Topperlearning
The equation is in standard form xf=x^ {3}4x^ {2}11x30 x f = x 3 − 4 x 2 − 1 1 x 3 0 Divide both sides by x Divide both sides by x \frac {xf} {x}=\frac {\left (x5\right)\left (x2\right)\left (x3\right)} {x} x x f = x ( x − 5) ( x − 2) ( x 3) Dividing by x undoes the multiplication by xFind stepbystep Engineering solutions and your answer to the following textbook question Determine the highest real root of $$ f(x) = x^3 6x^2 11x 61 $$ (a) Graphically (b) Using the NewtonRaphson method (three iterations, $$ x_i = 35 $$ ) (c) Using the secant method (three iterations, $$ x_{i1}= 25 $$ and $$ x_i = 35 $$ )Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music




Examples Int 3x 2 X 3 6x 2 11x 6 Dx




Evaluate Given F X 5x 2 And G X X 2 6x Chegg Com
(i) f(x) = x 3 – 6x 2 11x – 6, g(x) = x 2 x 1 Solution Given, f(x) = x 3 – 6x 2 11x – 6, g(x) = x 2 x 1 Thus, q(x) = x – 7 and r(x) = 17x 1 (ii) f(x) = 10x 4 17x 3 – 62x 2 30x – 3, g(x) = 2x 2 7x 1 Solution Given, f(x) = 10x 4 17x 3 – 62x 2 30x – 3 and g(x) = 2x 2 7x 1 Thus, q(x) = 5x 2 – 9x – 2 and r(x) = 53x – 123 Find roots (zeroes) of F (x) = x3 6x2 11x 6 Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F (x)=0 Rational Roots Test is one of the above mentioned tools It would only find Rational Roots that is numbers x which can be expressed as the quotient of two integers selected by ShasiRaj Best answer If g (x) is a factor of f (x), then the remainder will be zero that is g (x) = 0 g (x) = x 3 = 0 or x = 3 Remainder = f (3) Now, f (3) = (3)3 – 6 (3)2 11 x 3 – 6 = 27 – 54 33 – 6
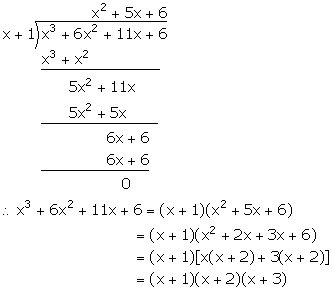



Chapter 8 Remainder And Factor Theorems Selina Concise Mathematics Part Ii Solutions For Class 10 Mathematics Icse Topperlearning



Factorise X 3 6x 2 11x 6 Completely Using Factor Theorem Sarthaks Econnect Largest Online Education Community
Algebracalculator 611x6x^2x^3=0 en Related Symbolab blog posts Middle School Math Solutions – Equation Calculator Welcome to our new "Getting Started" math solutions series Over the next few weeks, we'll be showing how Symbolab Example 2 Using factor theorem, factorize the polynomial x 3 – 6x 2 11 x – 6 Solution Let f (x) = x 3 – 6x 2 11x – 6 The constant term in f (x) is equal to – 6 and factors of – 6 are ±1, ± 2, ± 3, ± 6 Putting x = 1 in f (x), we have f (1) = 1 3 – 6 ×1 2 11× 1– 6 = 1 – 6 11– 6 = 0 ∴ (x– 1) is aF(x) = x 3 − 6x 2 11x − 6 g(x) = x 2 x 1 Here, degree f(x) = 3 and Degree (g(x)) = 2 Therefore, quotient q(x) is of degree 3 2 = 1 and the remainder r(x) is of degree less than 2 Let q(x) = ax b and r(x) = cx d Using division algorithm, we have f(x) = g(x) x q(x) r(x) x 3 − 6x 2 11x − 6 = (x 2 x 1)(ax b




Divide X 3 6x 2 11x 6 By X 2 X 1




If One Zero Of The Polynomial P X X3 6x2 11x 6 Is 3 Find The Other Two Zeros Brainly In
The sum of the values of a for which $$\frac{x^36x^211x6}{x^3x^210x8} \frac a{30} = 0$$ does not have a real solution is A $1$ B $12$ C $13$ D $2$ I tried to factorise the numerator and54 Find roots (zeroes) of F(x) = x 4 6x 3 11x 2 6 Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F(x)=0 Rational Roots Test is one of the above mentioned tools Factor f (x) = x3 − 6x2 11x − 6 f ( x) = x 3 − 6 x 2 11 x − 6 Click to expand There is the Rational Roots Theorem If a polynomial has a rational root, then it is of the form n d



F X X 3 6x 2 11x 6 G X X 2 X 1 Sarthaks Econnect Largest Online Education Community




Ml Aggarwal Solutions For Class 10 Maths Chapter 6 Factorization Access Free Pdf
23 Find roots (zeroes) of F(x) = x 36x 2 11x6 Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F(x)=0 Rational Roots Test is one of the above mentioned tools It would only find Rational Roots that is numbers x which can be expressed as the quotient of two integers TheLet the polynomials f and g be defined by f(x) = 3x^3 6x^2 11x and g(x) = 8x^2 15x 7 Which ofSolution Steps f ( x ) = x ^ { 3 } 3 x ^ { 2 } 6 x 8 f ( x) = x 3 3 x 2 − 6 x − 8 By Rational Root Theorem, all rational roots of a polynomial are in the form \frac {p} {q}, where p divides the constant term 8 and q divides the leading coefficient 1 One such root is 4 Factor the polynomial by dividing it by x4




In Each Of The Following Use Factor Theorem To Find Whether Polynomial G X Is A Factor Of Polynomial F X Or Not F X X 3 6x 2 11x 6 G X



F X X 6x 11x 6 G X X X 1 Find The Quotient Sarthaks Econnect Largest Online Education Community



Simplify Completely 8x 2 10x 3 X 2 9 4x 2 Chegg Com




If One Zero Of The Polynomial P X X 3 6x 2 11x 6 Is 3 Find The Other Two Zeros




X 3 6x 2 11x 6 0 Youtube




Lim X 1 X 2 3x 2 X 3 6x 2 11x 6



P X X 3 6x 2 11x 6 G X X 2 5x 6 Sarthaks Econnect Largest Online Education Community




Section 3 7 Proper Rational Functions Section 3 7 Proper Rational Functions Ppt Download




2 4 Zeros Of Polynomial Functions 1 7 Find All The Chegg Com




Fx X3 6x2 11x 6 Gx X 3 Fx 2x3 9x2 X 12 Gx X Gauthmath




F X X 3 6x 2 11x 6 G X X 3 Long Division Method Brainly In




Solve The Following Equations X 3 6x 2 11x 6 6 Youtube




Focus In High School Mathematics Reasoning And Sense Making Pdfdrive Com Flip Book Pages 51 100 Pubhtml5
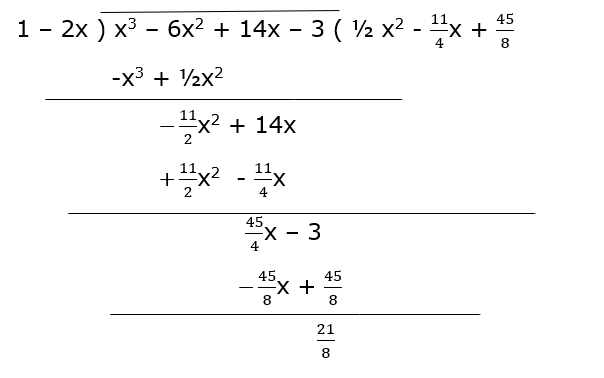



Ex 2 3 Q8 Find The Remainder When P X X 3 6x 2 14x 3 Is Divided By G X 1 2x




Ex 2 4 Q24b 𝑥3 6𝑥2 11𝑥 6 Factorise



Find The Integral Roots Of The Polynomial F X X 3 6x 2 11x 6 Sarthaks Econnect Largest Online Education Community




Factorise X 3 6x 2 11x 6 Using Factor Theorem Brainly In




Solve The Following Equations X 3 6x 2 11x 6 6




Biologia Zadania Przygotowawcze Do Egzaminu Z Matematyki Pdf Darmowe Pobieranie



1




Find The Remainder When P X 6x2 14x 3 Is Divided By Gor Scholr




Apply The Division Algorithm To Find The Quotient And Remainder On Dividing F X By G X F X Brainly In



How Would We Solve The Equation X 3 6x 2 11x 6 0 Quora




Factorize X 3 6x 2 11x 6 Youtube




If F X X 2 4 X 3 6x 2 11x 6 X 1 X Then Set Of Points At Which The Function If Non Differentiable Is




7 Find The Zeros Of The Polynomials G X3 6x2 11x 6 Ii Scholr




Module 1 Polynomial Functions




F X X 3 6x 2 11x 6g X X 2 Brainly In




Jak Rozwiazac Rownanie X 3 6x 2 11x 6 0 Brainly Pl




Find The Root Of The Equation X 3 6x 2 11x 6 0
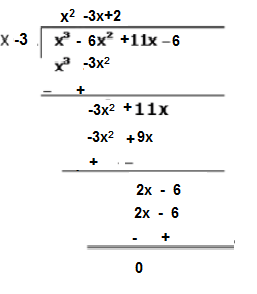



If One Zero Of The Polynomial P X X3 6x2 11x 6 Is 3 Find The Other Two Zeros Snapsolve
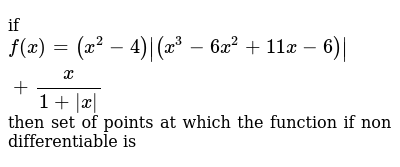



If F X X 2 4 X 3 6x 2 11x 6 X 1 X Then Set Of Points At Which The Function If Non Differentiable Is




R D Sharma Solutions Class 9th Ch 6 Factorization Of Polynomials Exercise 6 2
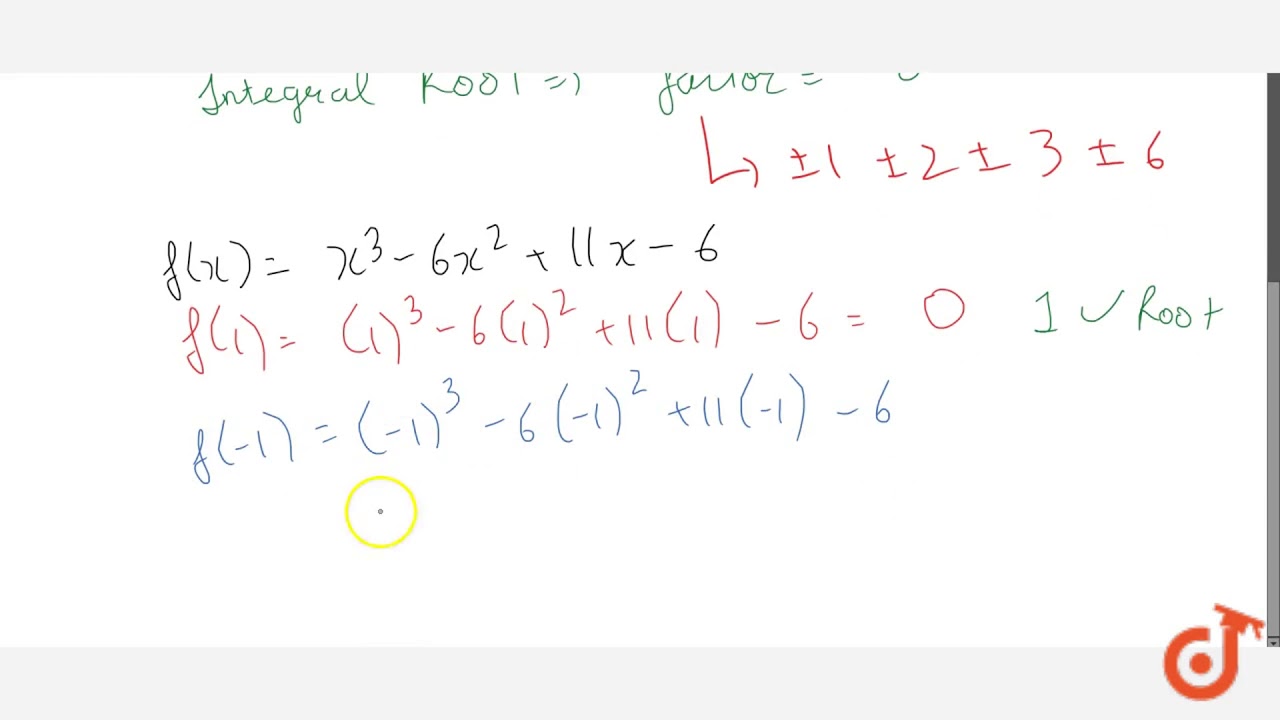



Find Integral Roots Of The Polynomial X 3 6x 2 11x 6 Youtube



If The Zeroes Of The Cubic Polynomial X3 6x2 3x 10 Are Of The Form A A B And A 2b For Some Real Numbers A And B




Fx X3 6x2 11x 6 Gx X 3 Fx 2x3 9x2 X 12 Gx X Gauthmath




Factorization Of Polynomials Using Factor Theorem A Plus Topper




Divide The Polynomial X3 6x2 11x 6 By X 3 And Check Whether X 3 Is A Factor Of The Polynomial Brainly In




F X X 3 6x 2 11x 6 G X X 3 Solve It Now For Using Factor Theorem Maths Polynomials Meritnation Com




Module 2 Polynomial Functions




Divide X 3 6x 2 11x 6 By X 2 8x 27



Search Q X3 6x2 2b11x 6 Divided By X 2b2 Tbm Isch




Rd Sharma Class 10 Solutions Maths Chapter 2 Polynomials Exercise 2 3



How Do You Factor X 3 6x 2 11x 6 Socratic




Master Math 18 College Algebra Fall B1 Chegg Com




Divide The Polynomial X3 6x2 11x 6 By X 3 And Check Whether X 3 Is A Factor Of The Polynomial Brainly In




Let F X X 2 3x 2 X 3 6x 2 11x 6 Sin X Pi 4 Number Of Points At Which The Function F X Is Non Differentiable In 0 2 Pi Is




Divide P X X3 6x2 11x 6 By G X X2 X 1 Brainly In




Ex 2 4 2 Use The Factor Theorem To Determine Whether Ex 2 4




Find Q X And R X On Dividing F X By G X F X X 6x 11x 6 G X X X 1 Equation Wise Maths Polynomials Meritnation Com




2



Http Math Arizona Edu Cjewell 122b Handouts Derivativepractice Pdf




Modulo Iv Aplicaciones De Las Derivadas Lesbia By Lesbia Perez Issuu



Mathscene Factorising Polynomials Lesson 1




Module 2 Polynomial Functions




Apply Division Algorithm To Find The Quotient Q X And Remainder R X Obtaimed On Dividing X3 6x2 11x 6 By X2 X 1 Ate I And 2 Maths Polynomials Meritnation Com
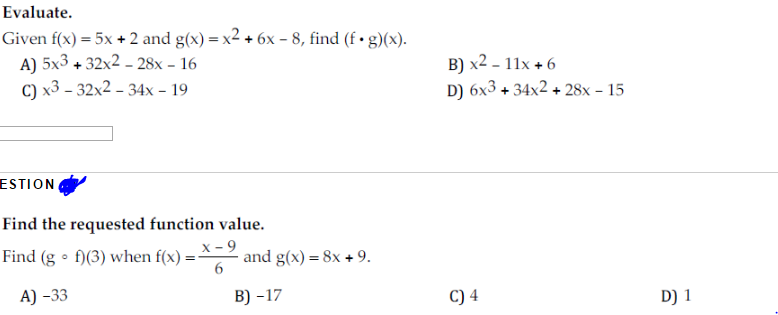



Given F X 5x 2 And G X X 2 6x 8 Find F Chegg Com




Factorise X3 6x2 11x 6 Completely Using Factor Theorem Mathematics Shaalaa Com




Problem 40 The Value S Of A For For Which X3 6x2 Math




Find The Remainder When P X 6x2 14x 3 Is Divided By Gor Scholr



Solved 5t Marks The Volume Of A Rectangular Box Is X3 6x2 11x 6 Cm3 The Box Is X 3 Cm Long And X 2 Cm Wide How High Is The Box Course Hero




3 P X 2x4 9x3 6x2 11x 6 G X X 1 Brainly In




F X X 3 6x 2 11x 6 G X X 2 Brainly In
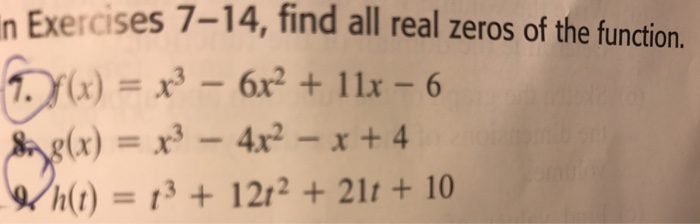



Find All Real Zeros Of The Function F X X 3 Chegg Com




Apply Division Algorithm To Find The Quotient Q X And Remainder R X Obtaimed On Dividing X3 6x2 11x 6 By X2 X 1 Ate I And 2 Maths Polynomials Meritnation Com




Divide F X X3 6x2 11x 6 By G X X2 X 1 Using Division Algorithm Youtube



By Remainder Theorem Find The Remainder When P X Is Divided By G X Studyrankersonline




Divide X 3 6x 2 11x 6 By X 2 And Verify The Division Algorithm



Http Www Npsd K12 Nj Us Cms Lib04 Nj Centricity Domain 156 2 3 the remainder and factor theorems Pdf




Apply The Division Algorithm To Find The Quotient And Remainder By Dividing F X By G X Where Brainly In




Numerical Methods For The Root Finding Problem Pdf Free Download



Q Tbn And9gcryclifmbfnva4pp2uht9xbcmzl7iwuj8isfuphjveji7ocq4uk Usqp Cau



Factorise X 3 6x 2 11x 6 Completely Using Factor Theorem Sarthaks Econnect Largest Online Education Community
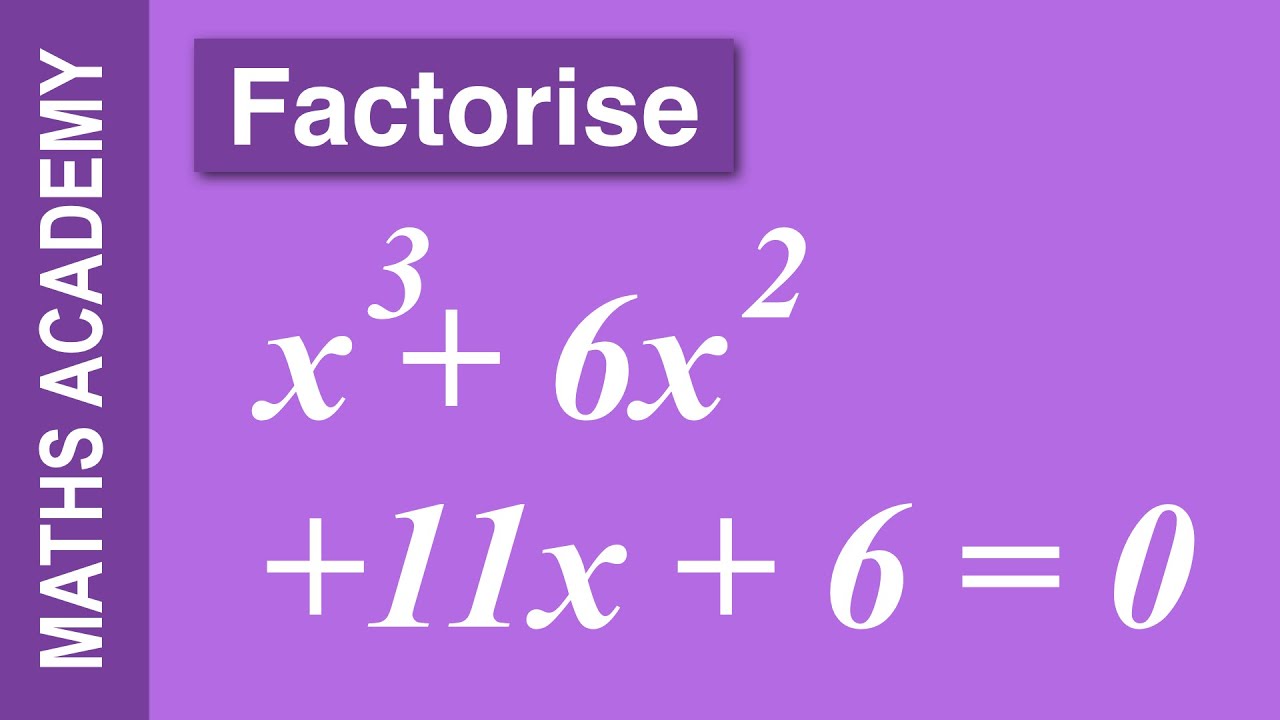



How To Factorise X 3 6x 2 11x 6 0 Youtube



If A Is Domain Of F X In Tan 1 X 3 6x 2 11x 6 Sarthaks Econnect Largest Online Education Community




Question Apply Division Algorithm To Find The Quotient Q X And Remainder R X On Dividing F X By G X In Each Of The Following I F X X 3 6 X 2 11 X 6 G X X 2 X 1



No comments:
Post a Comment